大家好!
这是一个全新的系列,也是厦门大学数学科学学院第一年开设的课程。希望这一个全新的系列能够让大家(当然也包括我自己……)从一个系统的角度来看优化这一个主题。同样,这也是专栏内目前的第一个真正与我的主修专业——计算数学相关的系列笔记。
数值优化 (Numerical Optimization)在目前大数据时代的重要性不言而喻。无论是统计学,运筹学,应用数学等传统数学系的方向,还是机器学习,深度学习等人工智能的方向,你都可以看到数值优化的影子。比方说很多人都一定听说过梯度下降法,也叫最速下降法,我们知道它能够成为一个好的优化方法,是因为负梯度是函数等高线上最“陡”的方向。但是问题是,最速下降法真的最速吗?实现的时候要在这个方向走多少?要回答这个问题实际上并不是那么容易。同样的,优化的应用性很强,这一点所有人都没有异议。但是优化的理论性同样也很强,换句话说,会大量依赖传统数学系的数分高代,数值分析等课程的知识。因为没有理论,就像夜空中没有那最亮的星一样,无法指引你前行(我唱出来了2333)。
我之前在专栏和公众号里还有提到过凸优化 (Convex Optimization)的更新计划。凸优化是优化的一个真子集,因此它的重点自然会更关注一些“凸”的方法。我们先更新数值优化,其实也是因为这一门课更像是内功,有了内功,学习凸优化的工具,也会更加得心应手。因此虽然时间上凸优化不一定会在数值优化更新完才出现,但是在阅读顺序上,我们还是建议大家先阅读数值优化这一个系列。当然如果对于已经熟悉这些内容的同学来说,自然也就无所谓了。
这一门课我们主要参考的是教授的笔记,主要的参考书会在每一节的开头列出。这一个系列笔记也是教授个人研究成果的总结,因此需要事先提醒大家的是,本系列的课程内容禁止任何形式的盗用,具体是什么形式,法律条文里面都有哈。
对了,这里恰个饭:如果小伙伴有需要更系统、完善的入门学习课程,推荐深蓝学院XX的专门课程:
机器人中的数值优化 - 深蓝学院 - 专注人工智能与自动驾驶的学习平台那么我们开始吧。
优化这个词对于很多人来说并不陌生。直观理解就是将一个事情不断做得更好,比方说在阿里,老板和你说“你被优化了”,意思就是你的离开对于公司来说更好(因为阿里可能需要更好的人),所以意思就是你被开除了。万事万物,如果我们把所有统计学家都干掉,不承认这个世界上存在随机性的话,都可以写成一个函数。那么优化的目标,就是要找到一个函数的极值,这个思维也会贯穿这个系列。当然,数学上来写,我们就是要考虑这么一个问题。
其中为可行域,
为一个
的实值函数。当然你求最大值也是可以的,因为本质上就是在求
在定义域上的最小值。同时,为了方便起见,我们之后不会刻意的说“求函数在定义域上的最小值”,而直接说求函数的最小值。
你理解了这个,你就理解了优化。但是和
有多少种可能?这个是很难说的。问题规模大吗?问题可解吗?解决方案的效率如何?有没有隐患?任何一个问题都能衍生出无数子问题出来。我们之后的每一个系列,其实目的都是解决一个特定的问题。而不同问题之间的比较,相信也会让大家对不同的方法和优化的理论有更深的理解。
既然我们提到了最小值,那么自然我们要关注一些更细节的定义
Definition 1: Global Minimizer
如果对任意的,都有
成立,那么
就是函数的全局最小值。
非常直观明了。同时,为了方便起见,我们说函数“取到最小值”,就是指函数取到全局最小值。
Definition 2: (Strict) Local Minimizer
如果对任意的,都有
成立,那么
就是函数的局部最小值。如果严格不取等,那么就称它为严格局部最小值。这里
称为
的邻域。
在数分一中我们学过,邻域就是包含它的一个无穷小量的球,也就是。换句话说,空间中任何一个与
距离小于
(小于等于也是可以的,这个细节不重要)的点,都在它的邻域,这里的
充分小(我喜欢将充分小理解为,令
,对于我的理论不会有破坏)。
还有一个概念可能比较陌生。我们也写在这里
Definition 3: Isolated Local Minimizer
如果是
的唯一局部最小值,则称它是孤立局部最小值。
一个很好的区分这两个概念的例子是这么一个函数
这里的是指它的左极限。这个函数不难看出,在
的时候取到最小值,它也是局部最小值,也是严格局部最小值。但是它并不是孤立局部最小值,因为
,这就相当于说,无论我这个邻域球取得多小,都会涵盖住
这个点(有理数的稠密性),而
也是局部最小值(这里有一个容易混的地方。根据定义,它是相对于
的局部最小值,但是如果相对
,它并不是最小值),这就说明了我们的结论。当然,这个例子也说明了,得到局部最小值和得到全局最小值是两码事。
接下来,我们给出一些与凸有关的定义。当然有的书上把它写成了下凸。
Definition 4: Convex Set
对于集合以及集合内的任意两点
,如果对任意的
,都有
,那就称集合是一个凸集。
下面这张图就很好的解释了凸的含义。右边的这个集合就不是凸集,因为它“凹”下去了,所以线段中间的部分就不属于那个集合了。
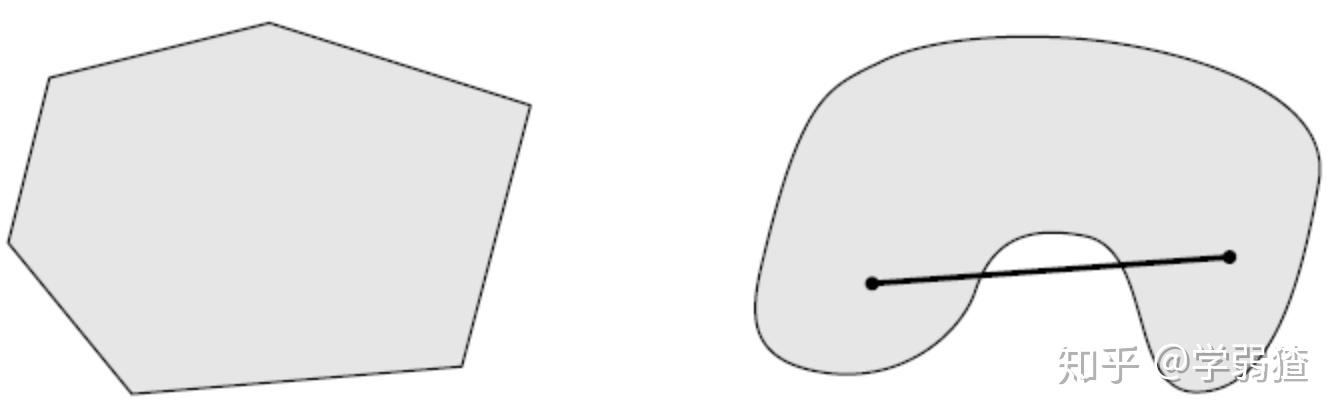
Definition 5: Convex Function
如果函数的定义域是一个凸集并且满足对任意
,有
,则称它是一个凸函数。
通过这个定义不难验证,对应的就是一个凹函数 (concave function),也就是很多书上写的上凸函数。
相信你在引入中已经可以看出来,我们所关注的优化问题已经不再是一元微积分里关注的内容。而更多的关注多元实值函数。这样的话,我们对应的函数求导,求积分等等,都会变成向量求导和向量积分。也就是变成了求梯度和求海塞矩阵。也正是如此,我们需要重新回头来看我们学过的求导运算。这一部分的内容极端重要,在人工智能领域也有很多应用。
在此之前,我们自然需要一些梯度和海塞矩阵的定义。
Definition 6: Gradient
, 定义
的梯度为一个
维向量,且对应的第
个分量为
Definition 7: Hessian
, 定义
的海塞矩阵为一个
维的矩阵,且对应的第
个分量为
根据这个定义,我们自然想到,如果我能够根据每一个分量求导,就能够求出梯度和海塞矩阵。这里我们给一个简单的例子。
Example 1
考虑,
,求
采用土的方法,将它的表达式拆出来,然后分量求导即可。注意到,所以可以得到
,因此拼在一起,就可以得到
。
但是这样做,实际上是很低效的,我们解一些简单的算例自然没有问题,但是实际问题上,我们这样做很多时候会破坏多元函数的一个整体性。因此我们通过介绍一些简单的性质来简化我们的运算。
Proposition 1:
设,且
,那么
,这里左边指的是方向导数
。
数分三中介绍过这个式子,其实就是方向导数的公式。
Proposition 2:
设,且
,那么
,这里左边指的是方向导数
。
这里的话只需要注意,每一个梯度的分量也都是一个多元函数即可。
有了这两个式子,结合一下方向导数最本质的极限定义,我们就不难得到我们的结论。
我们给出一个实际的例子
Example 2: Ridge Regression
考虑,
,
,求梯度与海塞矩阵。
熟悉的人会知道,这个就是岭回归的目标函数的一种形式。
有一部分我们已经求过梯度了,为
(注意
为常数),那么剩下的部分我们设为
,先根据Proposition 1,我们有
事实上,设,不难求得分子为
这一系列式子中我们可以忽略最后一项(因为的时候,最后一项为一个小量)。所以可以得到
这是因为根据题目条件,容易发现是一个数,因此求转置不会改变值。
因为我们的方向是任意取的,所以根据左右的对应,就可以得到我们的结论
,所以综合在一起,我们就可以得到
接下来,我们来计算海塞矩阵。也很容易,根据Proposition 2即可得到
(不要忘记写上单位阵),同样的根据的任意性,就可以得到
因此我们就证明完了结论。
学过岭回归的同学就知道,这里如果我们要求函数的最小值,那么令,可以得到
,而岭回归的情况下,
是正定的,因此运算合法,并且
处处正定,也就得到了函数的凸性和
确实是全局最小值的结论。
我们相信各位同学还会对矩阵求导很感兴趣,但是我们这里不再关注那么多,绝大部分的优化问题通过向量求导的工具就已经足够解决。当然我们如果在具体的例子中需要依赖矩阵求导的工具,我们会再回头来介绍它。
显然,如果要求极值,如果我们没有好的工具,也无从下手。事实上我们在上一部分的Example 2已经使用过,也就是说我们通过来找函数的极小值。但是这为什么是对的呢?多元函数的情况和一元函数类似吗?这就是我们要关心的部分。
在介绍相关性质之前我们还是先需要一些其它的结论。
Proposition 3: Taylor Expansion
设,
,那么存在
,使得
(1)
(2)
(3)
这事实上也就是多元泰勒展开的定义。刚开始可能大家不太熟悉,但是我们会反复用到它们,所以也不用担心。
同样,为了方便起见,我们不再说明这个事实。
好的,接下来我们会介绍一系列极值性质。
Proposition 4: First Order Necessary Condition
设,若
是一个局部最小值,那么
我们证明一下这个结论,联系一下一元微积分里面的结论,事实上导函数的直观意义就是斜率。对于一个最小值点,它的导函数为0也是直观上显然的。那么在梯度的意义下,如果我们要证明这个结论,只需要说明,若,这个点就不是极小值点就好,也就是说我们要说明还会存在更小的。而考察更小的可能,最稳妥的自然是负梯度方向,这也就是我们证明的思路。
如果说,那么考察一下负梯度方向
,就可以得到
(想想为什么),根据我们导函数的连续性可以推出梯度的连续性,也就是说存在一个较小的
,使得
接下来我们考虑在什么式子上我们会用到这个结论?事实上就是我们Proposition 3的第一个式子。注意到对于任意的,我们有
这里要注意我们的性质中,是任意的。因此我们就证明了结论。
仅仅这一个性质来说明极小值还不够,就像我们在Example 2中用了海塞矩阵一样,我们在这里也要考虑海塞矩阵带给我们的信息。
Proposition 5: Second Order Necessary Condition
设,若
是一个局部最小值,那么
这里要注意,如果说矩阵,就代表半正定。
完全相同的思路,如果说海塞矩阵在处非半正定,那就说明存在一个方向
,使得
,考虑一下Proposition 3的第二个式子并结合
即可,这里我们略去证明。
接下来我们加入函数的凸性,再介绍两个极值性质。
Proposition 6:
若是凸函数,那么局部最小值即为全局最小值。
还是依然考虑使用反证法,也就是说如果设为局部最小值,
为全局最小值,并且
,那么根据凸函数的性质,对于任意的
,有
我们稍作修改,可以得到,这说明什么?说明
是一个下降方向。为什么这样就不行了呢?这是因为,局部最小值是不允许出现下降方向的,否则会违背定义。因此结论成立。
Proposition 7:
若是凸函数,
,那么任何一个驻点都是全局最小值点。
这个直观上也很显然,也就是说,如果一个点不是全局最小值,那么我们只要证明它不是驻点即可(相当于使用了逆否条件)。
假如说点不是全局最小值点,
是全局最小值点,那么就有
。使用和Proposition 6同样的方法,不难得到结论
,也就是说
是
上的一个下降方向,也就是说这个点不是一个局部最小值点,那么自然不可能是驻点,这就得到结论了。
这里要补充说明一点的是,这个性质的证明还可以考虑使用Proposition 1,得到
所以可以得到。但是我们没有在Proposition 6中使用,这是因为我们没有
的条件,因此梯度不一定存在。
我们在证明中使用了一个概念叫下降方向,虽然直观上非常清晰,但我们还是需要给一下它的严格定义。
Definition 8: Descent Direction
设,
,如果对于充分小的
,有
,则称
是一个下降方向。
说到这里,我们需要提一句的是,除非函数是凸函数,否则任何一个优化方法都只能够求解局部最小值。也正是因为如此,求解全局最小值是一个异常困难的问题,也正是因为如此,优化方法才会如此火爆。
我们在之前介绍了很多性质,有的人可能会疑惑,既然我们有了这些定理,为什么我们还需要依赖优化的工具来求解函数极值呢?这是因为虽然我们可以说明是一个函数极值的必要条件,但是,真正的函数的
这个方程好解吗?答案是否定的,甚至于说可不可解都不知道(也就是说没有解析解)。因此我们往往需要在数值意义上,通过迭代的方法得到我们的驻点 (stationary point),也就是梯度为0的点。
顾名思义,收敛速度就是在考察一个优化方法的效率高低。我们要注意的是,每一个优化的方法,也就是用来求函数极值的方法,都有各自的优劣。其中一个因素就是速度,收敛的速度快或慢,自然会影响一个问题求解的效率高低。
实际问题中我们怎么考察收敛速度呢?一般会依赖如下定义。
Definition 9: Q-rate of convergence
设自变量第步的迭代点为
,且
,那么如果
(1),则称为次线性收敛速度。
(2),则称为线性收敛速度。
(3),
,则称为超线性收敛速度。
(4),
,则称为二次收敛速度。
可以看出,这个定义本质上是考察相邻两点的差值的商,因此我们称它为商收敛速度。
Definition 10: R-rate of convergence
设,且
,那么如果
(1),则称为次线性收敛速度。
(2),则称为
收敛速度。
(3),则称为线性收敛速度。
(4),则称为超线性收敛速度。
这个定义考察的则是函数差值的根号,因此我们称它为根号收敛速度。
到此,我们铺垫好了优化的所有的基础理论,接下来我们就可以根据这些工具,来介绍不同的优化方法了。
我们在
学弱猹:矩阵流形优化|笔记整理(4)——拉回,优化计算实例,指数映射中简单介绍过线搜索方法,它既可以认为是一个单独的方法,也可以认为是一类方法。说它是一个优化方法,是因为它本身通过一些条件的检查,本身就是一个完整的成体系的迭代方法。说它是一类方法,是因为很多其它的方法需要以线搜索作为先行,通过其它的修改使得优化方法的性质发生改变。
这样说其实还是挺抽象的,我们思考一个更本质的问题:如何用迭代方法做优化?本质上,既然是迭代方法,那么自然是一步一步来的。我刚开始在一个初始点,然后我通过迭代,每一步都比上一步的函数值减小一些,直到函数值不能够再更小了,是不是就可以得到一个局部最小值点了?
假如说我们现在在一个点上,接下来我们考察点
,我们的目标自然是希望
也就是要寻找下降方向。这里为步长,而
为搜索方向。你可以看出,任何一个依赖线搜索的方法,本质上都是关心这两个元素。要不就是希望找到一个合适的步长,要不就是希望找到一个合适的方向。比方说如果我们选取好搜索方向
,那么只要考虑步长的限制条件就好,这样得到的方法就是我们已经很熟悉的最速下降法。
很显然,要寻找下降方向,光一个式子是不够的,你没有任何其它分析的工具自然不行,因此我们还需要补一个结论。
Proposition 8:
设,
,如果
则
是一个在
点处的下降方向。
这个性质的证明和之前证明的方法一模一样,我们不再给出证明的细节。但是通过这个,其实你可以看出来,并不是一定要
才是下降方向,只需要搜索方向
与负梯度
成一个锐角即可。
在这一部分我们主要关注的是迭代方法的步长选取问题。换句话说,如何选取步长,才能使得迭代能够收敛到驻点?过大过小肯定都不行吧?要解决这个问题,事实上也需要很多铺垫,我们慢慢来看。
有了Proposition 8,我们就可以找下降方向了。这样就够了吗?好像依然是不行的。下面我们举一个例子来说明反例。
Example 3:
考虑函数,并设迭代初值
,使用最速下降法并设置步长为
,问迭代是否下降?迭代是否收敛至驻点?
这里要注意的是,使用最速下降法就是给定了每一步的方向为当前点的负梯度。那么这种情况下,相当于自变量迭代的公式为
这样的话,容易写出这个数列的通项公式为
代入计算函数值会发现每一步确实满足函数值在不断下降,但是数列的极限均为,换句话说就是迭代并没有收敛到驻点。
也许有些人会发现这个序列的问题所在了。正如级数求和有收敛和发散一说,函数不断的下降并不能导致下降的量的和足够的大。也就是说,我们需要一些条件,来保证我们的函数值真的能够充分下降。
首先我们介绍一下Armijo条件。
Definition 11: Armijo Condition
设,且设
,其中
。如果
,则
满足Armijo条件。
下面我们来图解一下这个条件。
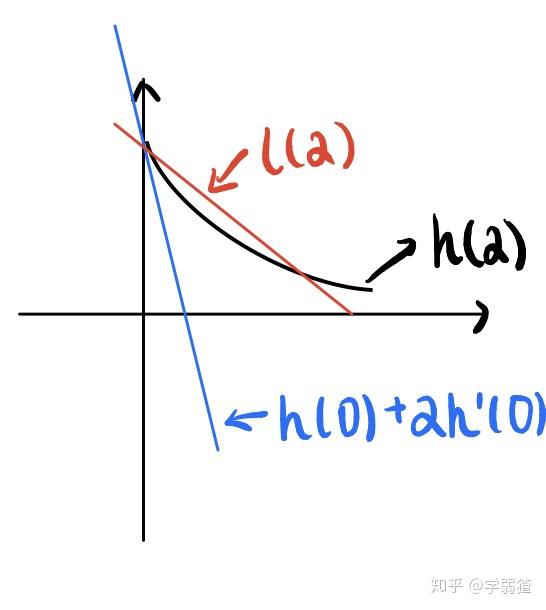
(注意黑线是,不是
,也就是说如果
一般是一个先减再增的函数,不然就不是下降方向了)。可以看出,蓝线就是在
处画的切线,而红线就是我们的
,那么根据Armijo条件,在红线下方的黑线那一部分就是满足条件的
。从直观上来看,因为它们在一条直线的下方,所以下降的程度比线性函数要快,因此可以认为是充分下降。
但是很遗憾,这个条件依然不足够用来作为满足全局收敛性(就是迭代收敛到全局最小值)的保证。我们同样给一个反例。
Example 4:
考虑与Example 3相同的函数和初始点,并考虑最速下降法。设步长,判断迭代是否满足Armijo条件,并判断迭代是否收敛至驻点?
在这里,我们同样的步骤可以得到数列迭代的通项公式为,可以看出,这个时候,取
,就能够得到
,
(注意到,其中
是当前的迭代点)。细节上不难验证满足充分下降的条件,但是你观察一下通项公式就知道数列的极限依然是
,所以依然不会收敛到驻点。
你可以看出来这个反例的产生源自于我们的步长选取过于保守。也就是说,我们的步长选取应该要大胆一些。这个思路就引导我们去考虑如下的Armijo-Goldstein条件。
Definition 12: Armijo Goldstein Condition
若步长满足
,并且
是集合
中最大的那个,
任意给定,且
,则称步长满足A-G条件。
在解释这个条件之前要多提一句这里“任意给定”的意思。这里的意思是我们的可以随便取,只要给定这个
之后,条件满足就可以。换句话说,假如说
,你选取了一个步长满足这个条件,那就够了。
下面我们解释一下这个条件。也就是说,我们的步长刚开始会设置为,然后我们第二步的选取,就在
中随便取一个,设为
,然后第三步就在
中随便取一个,设为
,以此类推就可以得到这样的序列。因为我们要的是集合中最大的那一个,所以我们事实上就是不断的尝试,从刚开始的步长开始,每一次都不断的缩小步长,直到步长满足A-G条件,我们就选取这个步长作为
并开始迭代。
有一种简易的方案,就是设,这个时候相当于给定了一个系数
,假如说我们的步长
太大了,导致无法满足A-G条件中的不等式,那么直接考虑
即可。这样的话,一方面,我们一开始的探索就会很大胆,另一方面我们也不会过于保守,因为只要我们达到条件,就会采用这个步长。具体的算法过程如下图

那么有没有其它的条件呢?答案当然是肯定的。我们这里再给出两个常用的步长选取条件
Definition 13: Weak Wolfe Conditions
如果步长满足
且
任意给定。则称它满足弱Wolfe条件。
还有一个条件与之对应
Definition 14: Strong Wolfe Conditions
如果步长满足
且
任意给定。则称它满足强Wolfe条件。
还是一样,画几张图就都明白了。
下一张图对应的是弱Wolfe条件。
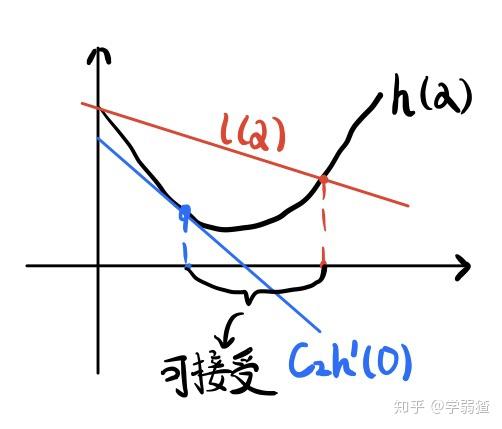
可以看出它还要求在每一步所选取的截取函数的斜率不断的增大(想想为什么)。注意到我们刚开始要选取一个下降方向,也就是说我们的截取函数的斜率都一定是负的。那么添加这个条件,就是要求斜率不要震荡。
为什么不允许震荡呢?看一下下面这张图。
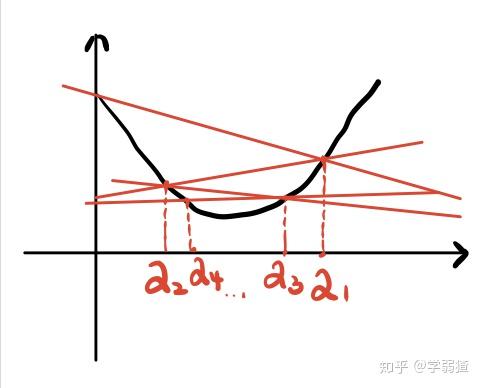
(这张图中黑线是,不是
)。可以看出,它的斜率在正负之间不断的切换,这样就会导致迭代点不断的左右横跳(Example 3),这个时候每一次都会使得函数值下降,但是并无法收敛到驻点。
那么强Wolfe条件说明了什么呢?还是看一下下面这张图
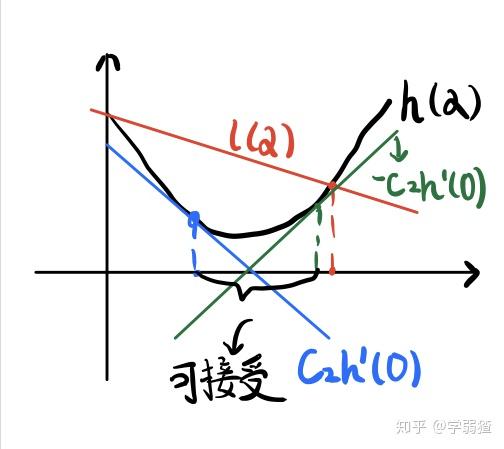
可以看出,除了要求每一次斜率必须增大以外,我还不允许斜率增加的特别大(因为这样有可能会使得下降不够充分)。因此实际上就比弱Wolfe条件要“更强了”。
再多嘴一句,因为出现了很多图,所以一定要区分黑线究竟是还是
。
好的,我们这一节先说到这里。
本节我们主要介绍了优化的基本理论和工具,包括极值的性质和一些求微分的工具。有了这些工具之后我们就开始探讨优化中,有关步长的优化方法的条件。在下一节我们会看到,不同的步长选取方法之间各有千秋,但它们都可以导致全局收敛性,具体的证明并不容易,我们下一节再说。
——————————————————————————————————————

本专栏为我的个人专栏,也是我学习笔记的主要生产地。任何笔记都具有著作权,不可随意转载和剽窃。
个人微信公众号:cha-diary,你可以通过它来获得最新文章更新的通知。
《一个大学生的日常笔记》专栏目录:笔记专栏|目录
《GetDataWet》专栏目录:GetDataWet|目录
想要更多方面的知识分享吗?可以关注专栏:一个大学生的日常笔记。你既可以在那里找到通俗易懂的数学,也可以找到一些杂谈和闲聊。也可以关注专栏:GetDataWet,看看在大数据的世界中,一个人的心路历程。我鼓励和我相似的同志们投稿于此,增加专栏的多元性,让更多相似的求知者受益~
电话:400-123-4567
传 真:+86-123-4567
手 机:13800000000
邮 箱:admin@eyoucms.com
地 址:广东省广州市天河区88号