优化器是在深度学习的反向传播过程中,指引损失函数(目标函数)的各个参数往正确的方向更新合适的大小,使得更新后的各个参数让目标函数不断逼近全局最小点。
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。每迭代一步,都要用到训练集所有的数据,如果样本数目很大,迭代速度很慢。
??优点:(1)迭代次数较少;(2)全局最优解;(3)易于并行实现;
缺点:(1)当样本数目很多时,训练过程会很慢。
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是仅仅选取一个样本j来求梯度。
??优点:(1)每次用一个样本更新模型参数,训练速度快;
(2) 有利于从局部最小值点跳到另一个局部最小值点,对于非凸函数,最终收敛于一个局部最小值点。
??缺点:
(1)随机梯度下降法用于仅仅用一个样本决定梯度方向,导致解很有可能不是最优解。
(2)对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。
SGD with momentum。参数更新时,不仅仅减去了当前迭代的梯度,还减去了前t-1迭代的梯度的加权和。由此可见,SGDM中,当前迭代的梯度,和之前迭代的累积梯度,都会影响参数更新。加入动量后,参数更新就可以保持之前更新趋势,而不会卡在当前梯度较小的点了。
SGDM认为梯度下降过程可以加入惯性。下坡的时候,如果发现是陡坡,那就利用惯性跑的快一些。SGDM全称是SGD with momentum。一阶动量是各个时刻梯度方向的指数移动平均值,也就是说, t时刻的下降方向,不仅由当前点的梯度方向决定,而且由此前累积的下降方向决定。
优点:
? ? ? ? (1)因为加入了动量因素,SGD-M缓解了SGD在局部最优点梯度为0,无法持续更新的问题和振荡幅度过大的问题,但是并没有完全解决,当局部沟壑比较深,动量加持用完了,依然会困在局部最优里来回振荡。
SGD 还有一个问题是困在局部最优的沟壑里面震荡。想象一下你走到一个盆地,四周都是略高的小山,你觉得没有下坡的方向,那就只能待在这里了。可是如果你爬上高地,就会发现外面的世界还很广阔。因此,我们不能停留在当前位置去观察未来的方向,而要向前一步、多看一步、看远一些。
NAG全称Nesterov Accelerated Gradient,是在SGD、SGD-M的基础上的进一步改进,我们知道在时刻t的主要下降方向是由累积动量决定的,自己的梯度方向说了也不算,那与其看当前梯度方向,不如先看看如果跟着累积动量走了一步,那个时候再怎么走。因此,在计算过程中,NAG不计算当前位置的梯度方向,而是计算如果按照累积动量走了一步,那个时候的下降方向:
 ?
?
然后用下一个点的梯度方向,与历史累积动量相结合,计算当前时刻的累积动量。
??优点:有利于跳出当前局部最优的沟壑,寻找新的最优值。
缺点:由于增加了计算步骤,导致收敛速度慢。
SGD系列的都没有用到二阶动量。二阶动量的出现,才意味着“自适应学习率”优化算法时代的到来。SGD及其变种以同样的学习率更新每个参数,但深度神经网络往往包含大量的参数,这些参数并不是总会用得到(想想大规模的embedding)。对于经常更新的参数,我们已经积累了大量关于它的知识,不希望被单个样本影响太大,希望学习速率慢一些;对于偶尔更新的参数,我们了解的信息太少,希望能从每个偶然出现的样本身上多学一些,即学习速率大一些。
怎么样去度量历史更新频率呢?那就是二阶动量——该维度上,记录到目前为止所有梯度值的平方和:
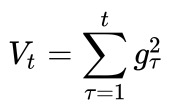
? ? ? ? 梯度下降步骤:?
![]()
![]() 。
。
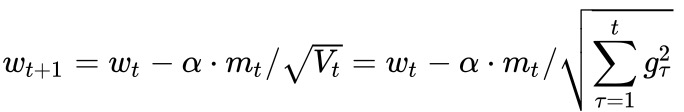
![]()
??优点:
(1)在稀疏数据场景下表现非常好
(2)此前的SGD及其变体的优化器主要聚焦在优化梯度前进的方向上,而AdaGrad首次使用二阶动量来关注学习率(步长),开启了自适应学习率算法的里程。
缺点:
(1)因为 是单调递增的,会使得学习率单调递减至0,可能会使得训练过程提前结束,即便后续还有数据也无法学到必要的知识。
由于AdaGrad单调递减的学习率变化过于激进,考虑一个改变二阶动量计算方法的策略:不累积全部历史梯度,而只关注过去一段时间窗口的下降梯度。这也就是AdaDelta名称中Delta的来历。

?
??优点:避免了二阶动量持续累积、导致训练过程提前结束的问题了。
SGD-M在SGD基础上增加了一阶动量,AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来,就是Adam了——Adaptive + Momentum。
SGD的一阶动量:
![]()
加上AdaDelta的二阶动量:
![]()
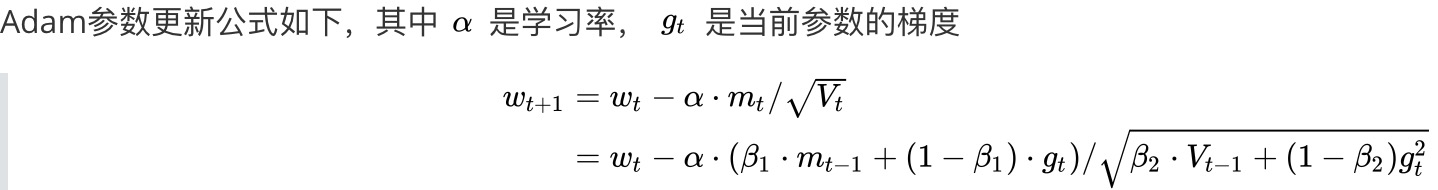 ?
?
优点:
(1)?优化算法里最常见的两个超参数![]() 就都在公式中,前者控制一阶动量,后者控制二阶动量。
就都在公式中,前者控制一阶动量,后者控制二阶动量。
? ? ? ? (2)通过一阶动量和二阶动量,有效控制学习率步长和梯度方向,防止梯度的振荡和在鞍点的静止。
??缺点:
(1)可能不收敛:二阶动量是固定时间窗口内的累积,随着时间窗口的变化,遇到的数据可能发生巨变,使得可能会时大时小,不是单调变化。这就可能在训练后期引起学习率的震荡,导致模型无法收敛。
修正的方法:由于Adam中的学习率主要是由二阶动量控制的,为了保证算法的收敛,可以对二阶动量的变化进行控制,避免上下波动。
![]()
?通过这样修改,就保证了 ![]() ,从而使得学习率单调递减。
,从而使得学习率单调递减。
电话:400-123-4567
传 真:+86-123-4567
手 机:13800000000
邮 箱:admin@eyoucms.com
地 址:广东省广州市天河区88号