最近遇到了一个数学优化问题,存在以下难点
目前尝试了很多算法,比如梯度下降,牛顿法和拟牛顿法,阻尼最小二乘等,信赖域方法,还有智能优化算法,比如遗传算法,差分进化等。但是这些算法效果很差,速度也很慢。最重要的是第二点,很难处理。
想请教下有没有前辈遇到过相似的科研问题或者是工程问题,望指点一二。感谢推荐论文或者书籍等材料哇,球球了!
可以试试加一些正则项,看看能不能让目标函数的性质变好一点。
multi-start可以试试,但估计不太能解决问题。
设计一个高效的数值优化算法需要考虑以下几个方面:
1. 函数的可导性:如果函数可导,则可以使用梯度信息来指导搜索方向和步长,从而提高算法的收敛速度。
2. 确定优化问题的目标函数:确保目标函数能够准确地衡量预期的优化结果,并且具有良好的性质,例如光滑、凸性等。
3. 选择合适的优化算法:根据问题的特点选择合适的优化算法,例如梯度下降、牛顿法、共轭梯度法等。
4. 设置合理的停止准则:根据优化问题的要求,设定合理的停止准则,例如达到指定的精度、超出最大迭代次数等。
5. 初始化参数:合理选择初始解的取值,可以参考先验知识或者使用随机生成的方式。
6. 调整步长和搜索方向:根据优化算法的特性,调整步长和搜索方向,使得算法能够快速收敛,避免陷入局部最优解。
7. 并行化技术:利用并行化技术,例如多线程、多进程等,加速优化算法的执行速度。
8. 算法优化和加速:根据实际问题的特点,对优化算法进行优化和加速,例如使用近似计算、剪枝操作等。
9. 参数调优:根据实际问题的特点,对优化算法的参数进行调优,选择合适的参数取值,提高算法的性能。
当设计一个高效的数值优化算法时,我们可以使用Python编写一个示例。以下是一个使用梯度下降算法来最小化目标函数的例子:
如果对你有帮助,请收藏和点赞,笔耕不辍。
import numpy as np
def objective_function(x):
# 定义目标函数,这里以简单的二次函数为例
return x**2
def gradient(x):
# 计算目标函数的梯度,这里是对目标函数求导得到的梯度
return 2*x
def gradient_descent(initial_x, learning_rate, num_iterations):
x=initial
for i in range(num_iterations):
# 计算当前点的梯度
grad=gradient(x)
# 更新参数
x -=learning_rate * grad
return x
# 设置初始点、学习率和迭代次数
initial_x=3
learning_rate=0.1
num_iterations=100
# 进行梯度下降优化
optimal_x=gradient_descent(initial_x, learning_rate, num_iterations)
print("Optimal solution: x=", optimal_x)
print("Optimal value: f(x)=", objective_function(optimal_x))
在这个示例中,我们定义了一个二次函数作为目标函数。然后通过计算目标函数的梯度,使用梯度下降算法来更新参数x。
看起来你不想要stationary point,这样global convergence条件的各种alm不适合你。
DAG已知的话,如果变量维数不高中间量多,可以试试maingo。如果变量维数高,中间量一般,可以试试baron。如果没有sin cos可以试试antigone,如果多项式比较多接近pop,可以试试各种魔改的rlt以及sdp-socpRelaxation。我记得新版maingo支持gams model了,不过maingo的一个问题是他的upper bounding problem基于ipopt加multi start。如果你的问题ill condition可能还需要特别多考虑,得看你的具体形式。如果你的dag连bilinear 项都没有,那可能我正做的superposition estimator是最可能求解的。
单个无人机三维路径规划问题及其建模_IT猿手的博客-CSDN博客
参考文献:
[1]胡观凯,钟建华,李永正,黎万洪.基于IPSO-GA算法的无人机三维路径规划[J].现代电子技术,2023,46(07):115-120
高尔夫优化算法(Golf Optimization Algorithm,GOA)由Montazeri Z等人于2023年提出,该算法模拟高尔夫运动过程中的球员击打高尔夫所采取的战术策略,能够有效平衡全局搜索和局部搜索的能力。
https://blog.csdn.net/weixin_46204734/article/details/132939196
参考文献:
[1]Montazeri Z, Niknam T, Aghaei J, Malik OP, Dehghani M, Dhiman G. Golf Optimization Algorithm: A New Game-Based Metaheuristic Algorithm and Its Application to Energy Commitment Problem Considering Resilience. Biomimetics. 2023; 8(5):386. Biomimetics | Free Full-Text | Golf Optimization Algorithm: A New Game-Based Metaheuristic Algorithm and Its Application to Energy Commitment Problem Considering Resilience
(1)部分代码
close all
clear
clc
addpath('https://www.zhihu.com/question/Algorithm/')%添加算法路径
warning off;
%% 三维路径规划模型定义
global startPos goalPos N
N=2;%待优化点的个数(可以修改)
startPos=[10, 10, 80]; %起点(可以修改)
goalPos=[80, 90, 150]; %终点(可以修改)
SearchAgents_no=30; % 种群大小(可以修改)
Function_name='F1'; %F1:随机产生地图 F2:导入固定地图
Max_iteration=50; %最大迭代次数(可以修改)
% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);
[Best_score,Best_pos,curve]=GOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj);%算法优化求解
AlgorithmName='GOA';%算法名字
figure
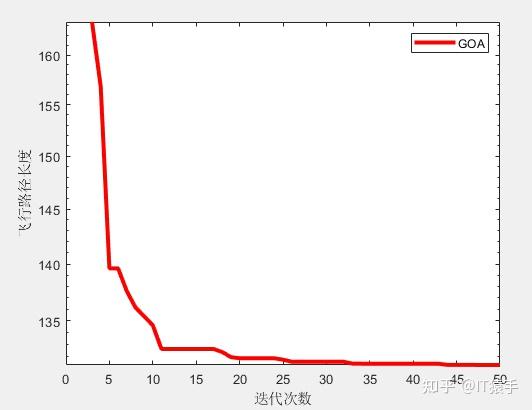
semilogy(curve,'Color','r','linewidth',3)
xlabel('迭代次数');
ylabel('飞行路径长度');
legend(AlgorithmName)
display(['算法得到的最优适应度: ', num2str(Best_score)]);
Position=[Best_pos(1:dim/3); Best_pos(1+dim/3:2*(dim/3)); Best_pos(1+(2*dim/3):end)]'; %优化点的XYZ坐标(每一行是一个点)
plotFigure(Best_pos,AlgorithmName)%画最优路径
(2)部分结果
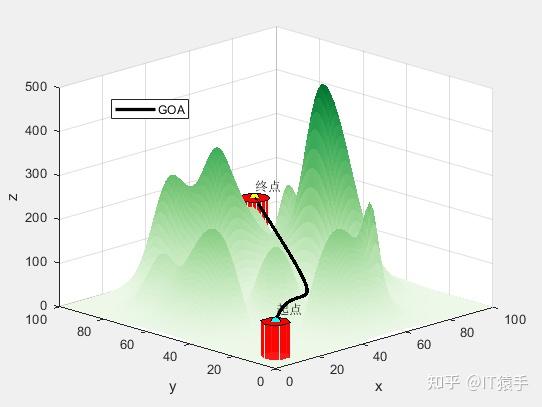
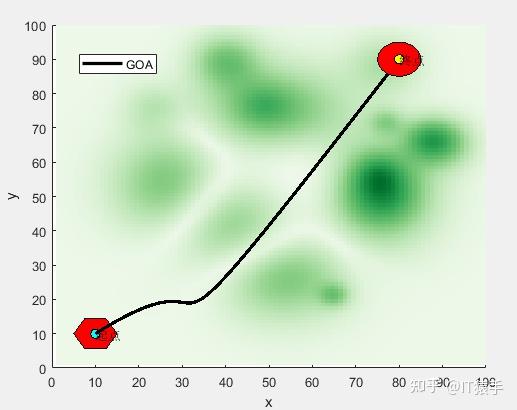
无人机飞行路径坐标:
1.0000000e+01 1.0000000e+01 8.0000000e+01
1.1376377e+01 1.1081252e+01 8.1066953e+01
1.2685431e+01 1.2078936e+01 8.2073506e+01
1.3929295e+01 1.2996239e+01 8.3021832e+01
1.5110102e+01 1.3836349e+01 8.3914103e+01
1.6229985e+01 1.4602452e+01 8.4752492e+01
1.7291078e+01 1.5297736e+01 8.5539171e+01
1.8295514e+01 1.5925389e+01 8.6276314e+01
1.9245426e+01 1.6488598e+01 8.6966091e+01
2.0142946e+01 1.6990550e+01 8.7610677e+01
2.0990209e+01 1.7434432e+01 8.8212243e+01
2.1789347e+01 1.7823433e+01 8.8772963e+01
2.2542493e+01 1.8160739e+01 8.9295007e+01
2.3251782e+01 1.8449538e+01 8.9780551e+01
2.3919345e+01 1.8693017e+01 9.0231764e+01
2.4547316e+01 1.8894364e+01 9.0650822e+01
2.5137828e+01 1.9056766e+01 9.1039894e+01
2.5693015e+01 1.9183410e+01 9.1401156e+01
2.6215009e+01 1.9277484e+01 9.1736778e+01
2.6705944e+01 1.9342175e+01 9.2048933e+01
2.7167953e+01 1.9380671e+01 9.2339795e+01
2.7603169e+01 1.9396159e+01 9.2611535e+01
2.8013725e+01 1.9391826e+01 9.2866326e+01
2.8401755e+01 1.9370859e+01 9.3106341e+01
2.8769391e+01 1.9336447e+01 9.3333752e+01
2.9118766e+01 1.9291776e+01 9.3550731e+01
2.9452015e+01 1.9240034e+01 9.3759452e+01
2.9771270e+01 1.9184409e+01 9.3962086e+01
3.0078664e+01 1.9128087e+01 9.4160807e+01
3.0376330e+01 1.9074256e+01 9.4357787e+01
3.0666402e+01 1.9026103e+01 9.4555198e+01
3.0951013e+01 1.8986816e+01 9.4755213e+01
3.1232295e+01 1.8959583e+01 9.4960004e+01
3.1512383e+01 1.8947590e+01 9.5171745e+01
3.1793409e+01 1.8954024e+01 9.5392607e+01
3.2077506e+01 1.8982075e+01 9.5624763e+01
3.2366808e+01 1.9034928e+01 9.5870386e+01
3.2663448e+01 1.9115771e+01 9.6131648e+01
3.2969559e+01 1.9227791e+01 9.6410722e+01
3.3287273e+01 1.9374177e+01 9.6709780e+01
3.3618725e+01 1.9558115e+01 9.7030995e+01
3.3966048e+01 1.9782792e+01 9.7376539e+01
3.4331374e+01 2.0051396e+01 9.7748585e+01
3.4716836e+01 2.0367115e+01 9.8149306e+01
3.5124569e+01 2.0733136e+01 9.8580873e+01
3.5556705e+01 2.1152646e+01 9.9045460e+01
3.6015377e+01 2.1628832e+01 9.9545239e+01
3.6502719e+01 2.2164883e+01 1.0008238e+02
3.7020863e+01 2.2763985e+01 1.0065906e+02
3.7571943e+01 2.3429325e+01 1.0127745e+02
3.8158092e+01 2.4164092e+01 1.0193973e+02
3.8781443e+01 2.4971472e+01 1.0264806e+02
3.9444129e+01 2.5854653e+01 1.0340461e+02
4.0148284e+01 2.6816823e+01 1.0421157e+02
4.0896040e+01 2.7861168e+01 1.0507109e+02
4.1689531e+01 2.8990876e+01 1.0598537e+02
4.2530890e+01 3.0209135e+01 1.0695656e+02
4.3422251e+01 3.1519132e+01 1.0798683e+02
4.4365745e+01 3.2924053e+01 1.0907838e+02
4.5363507e+01 3.4427088e+01 1.1023335e+02
4.6417670e+01 3.6031422e+01 1.1145394e+02
4.7530367e+01 3.7740244e+01 1.1274231e+02
4.8703730e+01 3.9556740e+01 1.1410062e+02
4.9939894e+01 4.1484099e+01 1.1553107e+02
5.1240991e+01 4.3525507e+01 1.1703581e+02
5.2609155e+01 4.5684153e+01 1.1861702e+02
5.4046518e+01 4.7963222e+01 1.2027688e+02
5.5555214e+01 5.0365903e+01 1.2201755e+02
5.7137376e+01 5.2895384e+01 1.2384120e+02
5.8795137e+01 5.5554850e+01 1.2575002e+02
6.0530630e+01 5.8347491e+01 1.2774617e+02
6.2345989e+01 6.1276493e+01 1.2983183e+02
6.4243347e+01 6.4345044e+01 1.3200917e+02
6.6224837e+01 6.7556330e+01 1.3428035e+02
6.8292591e+01 7.0913540e+01 1.3664756e+02
7.0448744e+01 7.4419861e+01 1.3911297e+02
7.2695428e+01 7.8078480e+01 1.4167874e+02
7.5034777e+01 8.1892585e+01 1.4434706e+02
7.7468923e+01 8.5865362e+01 1.4712009e+02
8.0000000e+01 9.0000000e+01 1.5000000e+02
(四)基于高尔夫优化算法GOA求解无人机三维路径规划研究(MATLAB) - 哔哩哔哩 (bilibili.com)
文章来源于我的个人GZH(见简介):KAU的云实验台,主要更新智能优化算法的原理、应用、改进
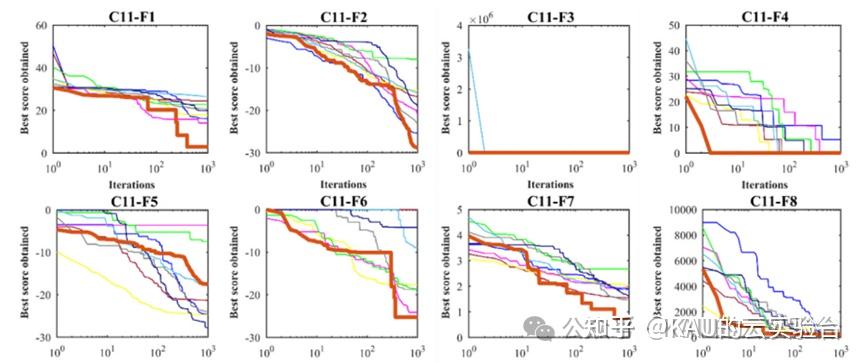
CEC2005中的测试
本文KAU将介绍一个2023年1月发表在中科院1区KBS上的优化算法——长鼻浣熊优化算法(Coati Optimization Algorithm,COA)[1]

该算法由Dehghani教授等人[1]于2023年提出,其模拟了北美长鼻浣熊合作攻击鬣蜥时的行为(勘探)以及分散逃离捕食者时的行为(开发),具有无需设置控制参数、高效率以及较强的平衡能力(勘探/开发)等优势,与11种优化算法在51个基准函数上进行测试,显示出其惊艳的性能。
图源文献[1]
本文将介绍COA原理、利用与改进,最后也给出了算法的MATLAB和Python实现。将这样性能优异的新算法应用于一些工程问题也能够在一定程度上提升文章的创新性。
00 目录
1 长鼻浣熊优化 (COA) 算法原理
2 代码目录
3 算法性能
4 源码获取
01 长鼻浣熊优化 (COA)算法原理
COA通过合作狩猎鬣蜥以及分散逃离捕食者两种行为来实现模型参数的优化,原理?如下:
1.1 勘探---合作狩猎鬣蜥
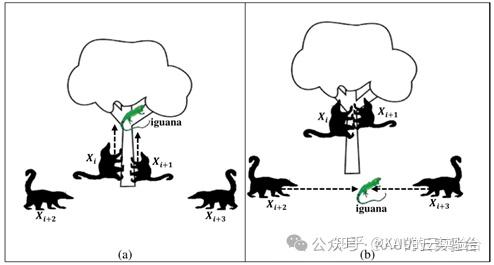
图源文献[1]
在该阶段,一半的长鼻浣熊爬上一棵树接近鬣蜥进行狩猎,同时另一半长鼻浣熊会聚集在树下游走等待鬣蜥落地,当鬣蜥落地,长鼻浣熊将猎杀它,鬣蜥即代表了全局最优位置,这种求解过程展现了COA的全局探索能力。
爬树长鼻浣熊行为的数学模型为:
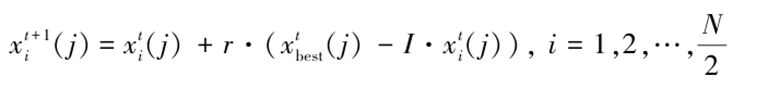
鬣蜥落地位置随机,地面长鼻浣熊也将据此随机移动,其数学模型为:
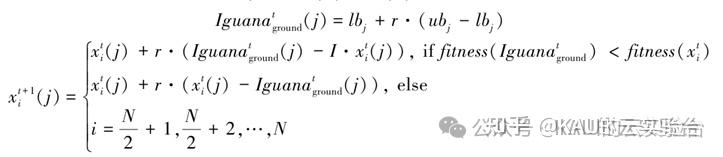
式中I为随机整数。
1.2 开发---分散逃离捕食者
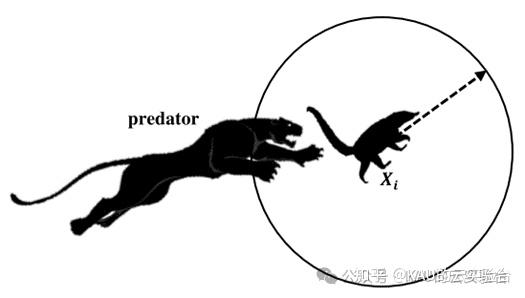
图源文献[1]
若出现捕食者攻击长鼻浣熊,则长鼻浣熊将逃离原来的位置,并在附近的安全地点寻求庇护。这反映了COA在局部搜索方面的性能,其数学模型为:
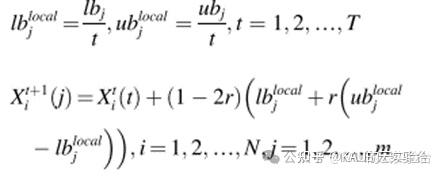
每次移动后,都将采用贪婪策略进行位置更新,即:
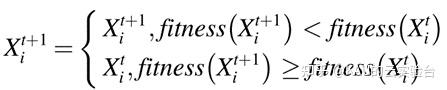
1.5 算法流程
COA算法已介绍完毕,包括勘探和开发两个阶段,结构简明,并且性能也不错,后续KAU也会推出COA的原创改进。该算法的的程图如下:

1.6 算法利用&改进
利用方面,COA的勘探阶段设计的比较有意思,其将种群分为两拨,各自执行不同的公式,前1/2受到了种群信息的引导,后1/2则进行分散的随机搜索,种群既能得到一定引导信息,同时也能分散扩大搜索范围,使得种群具有良好的全局性能,这一种策略可以加以利用。并且可以看到COA在开发阶段更倾向于在自身周围进行细致搜索,因此其全局最优的引导信息都落在了勘探阶段,进一步可以看到勘探阶段的重要性,想必将其引入其他算法中也能取得效果。
改进方面,可以注意COA的开发阶段,其主要是在当前个体周围进行搜索,没有种群信息的引导,可能不利于后期的收敛,可以引入全局最优信息对公式进行改进。后续KAU也将对COA算法进行原创改进,感兴趣的朋友可以关注一波哦~
02 代码目录
(左Python,右Matlab)
代码包含MATLAB和Python,Python代码为KAU按照原作者的Matlab代码手搓而成。考虑到很多同学获取代码后,MATLAB代码部分有乱码(MATLAB版本问题),有几个方法:
①可以将MATLAB版本改为2020及以上;
②将m文件用记事本打开,再将记事本中的代码复制到Matlab即可
代码都经过作者重新注释,代码清爽,可读性强。
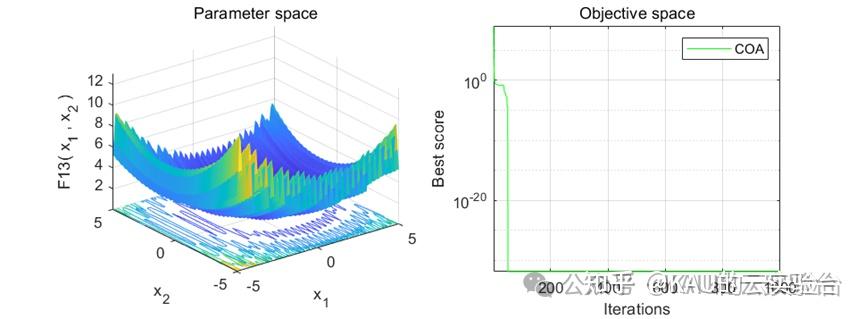
03 算法性能
采用标准测试函数初步检验其寻优性能
在MATLAB中,进行标准函数的测试,执行程序结果如下:
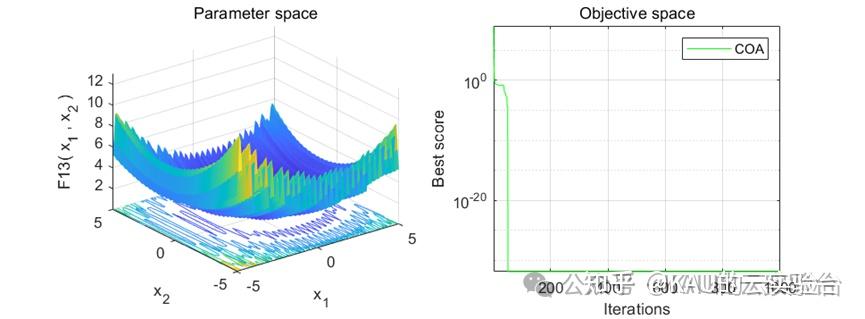
在Python中,进行标准函数的测试,执行程序结果如下:
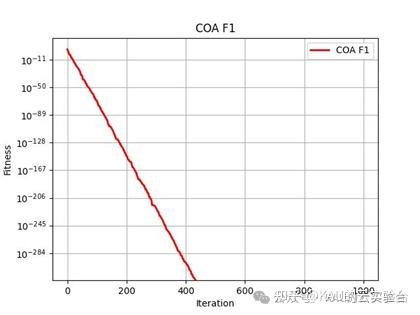
MATLAB和Python都进行了函数测试,测试效果都不错,其收敛速度和精度很好。
04 源码获取
在GZH(见简介)后台回复 COA 即可
后续KAU将更新关于COA的原创改进算法,感兴趣的话可以关注不迷路~
参考文献
[1]DEHGHANI M, MONTAZERI Z, TROJOVSKá E, et al.Coati Optimization Algorithm: a new bio-inspired metaheuristic algorithm for solving optimization problems[J].Knowledge-based systems, 2023, 259: 110011.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(? _)?(不点也行),你们的鼓励就是我坚持的动力!若有定制需求,可私信作者。
电话:400-123-4567
传 真:+86-123-4567
手 机:13800000000
邮 箱:admin@eyoucms.com
地 址:广东省广州市天河区88号